프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
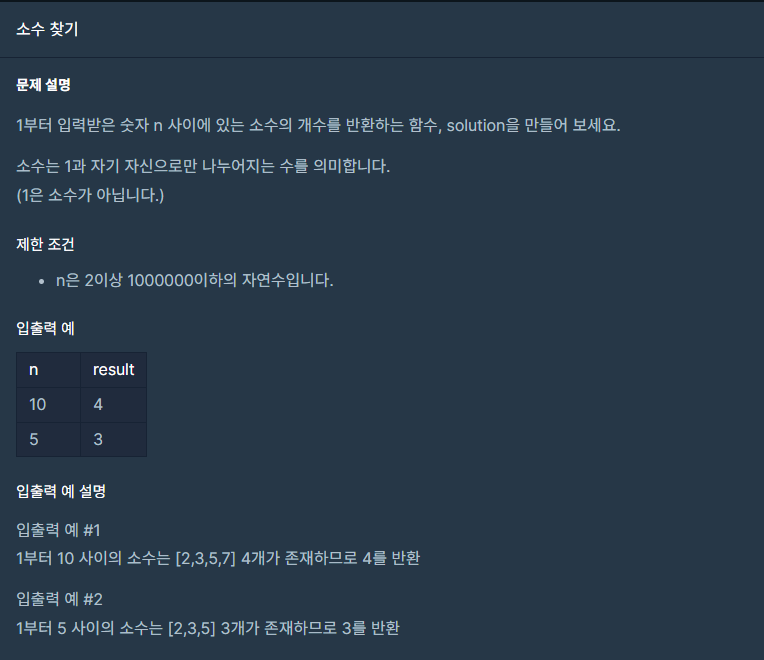
1. 구해야 하는 것
# 1부터 n사이의 소수
2. 1을 구하기 위해 필요한 것
# 소수를 구하는 방법
# 에라토스테네스의 체
# 직접 나눠서 세기(제곱근까지)
# 관련 모듈이 있을까? > 못찾음
3. 그 외 고려해야 할 사항
# n은 1000000이하의 자연수(시간복잡도 고려)
단순히 전체 수를 돌면서 약수면 카운트를 올려서 약수가 없는 수만 골라내는 방법(시간 초과)
def solution(n):
count = 0
answer = 0
for i in range(3, n+1):
for j in range(2, int(i ** 0.5) + 1):
if i % j == 0:
count += 1
if count == 0:
answer += 1
count = 0
return answer + 1
에라토스테네스의 체
# 에라토스테네스의 체
#
# 핵심은 소수의 배수를 지워나가는 것.
# 2부터 시작해서 2 4 6 8 ... 을 지우고
# 다음 소수인 3의 배수 3 9 15 ...을 지우고(6과 12는 앞에서 이미 지워짐)
# ...
# 결국 소수만 남는다.
n = 20
# 0부터 n까지 인덱스로 표현할 배열 생성
# (인덱스 매칭의 편의성을 위해 n+1개)
numbers = [True]*(n+1) # True면 소수, 소수로 나눠지면 False로 바꿔줄 예정
# 0과 1은 소수가 아님
numbers[0], numbers[1] = False, False
# 2부터 n까지 돌면서(n의 제곱근까지만 돌아도 ok)
for i in range(2, int(n ** 0.5) + 1):
if numbers[i]==True: # 특정 수가 지워지지 않았다면 (소수여서)
k = 2 # i * 1은 자기자신(소수)이므로 2부터 시작
# i의 배수를 지워주는 작업 i*2 i*3 i*4 ... n이하의 모든 배수를 지워준다.
while (i * k) <= n: # i * k가 n보다 커질때까지 반복
numbers[i*k] = False
k += 1
for i in range(len(numbers)):
if numbers[i]:
print(i, end=' ')
# 왜 제곱근까지만 해도 되는지?
# n = 144(12*12)일 때,
# 2 4 6 8 ...
# 3 9 15 21 ...
# 4 pass (4는 False이므로)
# 5 25(5*5) 35(5*7) 55(5*11) ...
# 6 pass
# 7 49(7*7) 77(7*11)
# 8 pass
# 9 pass
# 10 pass
# 11 11*11 11*13 11*17 ...
# 해당 수보다 작은 소수와의 곱은 이전에 모두 지워지게 된다 ex)3*7은 3에서 다 지워져서 7에서는 고려할 필요가 없음
# 자신보다 큰 소수와의 곱만 지워주면 된다. 따라서 제곱근까지만 판별하면 소수를 모두 판별할 수 있다.
# 완성된 함수
def solution(n):
numbers = [True]*(n+1)
numbers[0], numbers[1] = False, False
for i in range(2, int(n ** 0.5) + 1):
if numbers[i]:
k = 2
while (i * k) <= n:
numbers[i*k] = False
k += 1
return numbers.count(True)
에라토스테네스의 체와 차집합 연산을 사용한 방법
def solution(n):
num=set(range(2,n+1))
for i in range(2,int(n ** 0.5) + 1):
if i in num:
num-=set(range(2*i,n+1,i)) # 현재의 소수(i)의 배수를 집합(num)에서 제거
return len(num)'코딩 테스트 연습' 카테고리의 다른 글
| [알고리즘] 프로그래머스 - 과일 장수 (0) | 2023.05.19 |
|---|---|
| [알고리즘] 프로그래머스 - 푸드 파이트 대회 (0) | 2023.05.19 |
| [알고리즘] 프로그래머스 - 카펫 (0) | 2023.05.09 |
| [알고리즘] 프로그래머스 - 괄호 회전하기 (0) | 2023.05.08 |
| [알고리즘] 프로그래머스 - 기사단원의 무기 (0) | 2023.05.08 |




댓글